[백준 3009] 네 번째 점 C Python

3009번 - 네 번째 점

문제 이해

축에 평행한 직사각형의 네 점중 세 점만이 주어지고, 네 번째 점을 구하면 되는 문제

접근

문제의 예시를 그림으로 나타내면 다음과 같다. 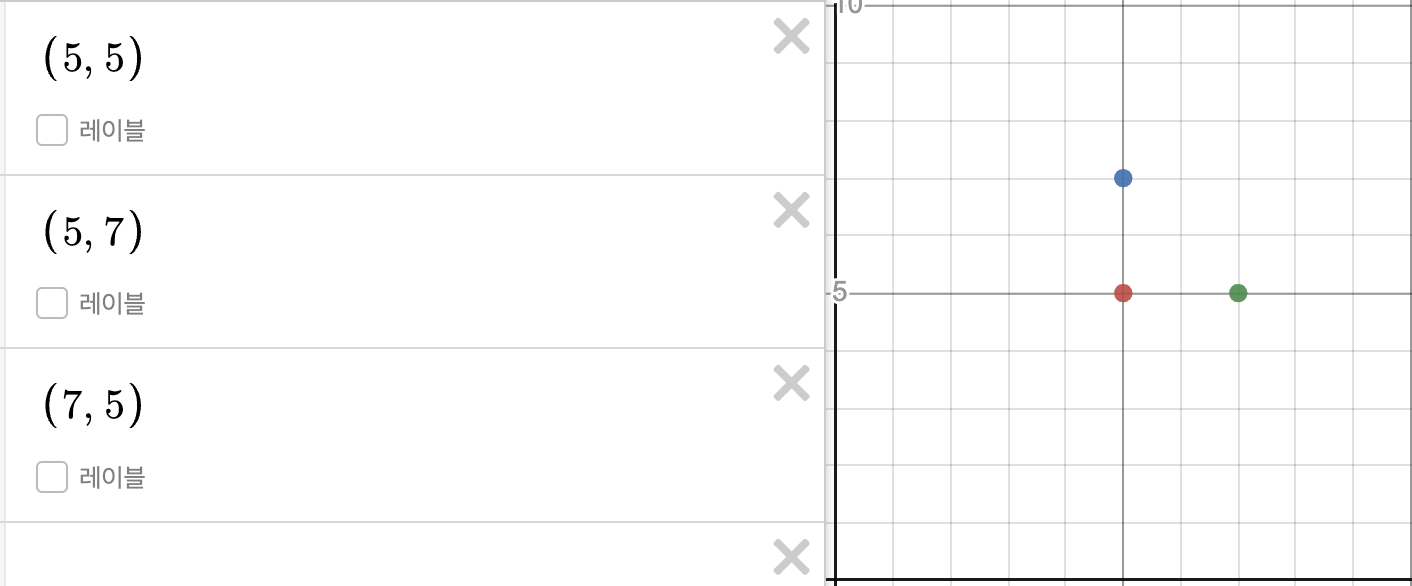(x1, y1), (x1, y2), (x2, y1)으로 주어지면, 답은 (x2, y2)가 된다. 세 점이 어떻게 주어지든, 각각의 x와 y를 따로 생각해 중복되지 않은 (두번 사용하지 않은) 좌표를 답으로 구해내면 된다.

정답 코드 - 방법 1: 구현 Python

x = []
y = []
for _ in range(3):
    b = list(map(int, input().split()))
    x.append(b[0])
    y.append(b[1])
for i in x:
    if x.count(i)==1:
        _x = i
for i in y:
    if y.count(i)==1:
        _y = i
print(_x,_y)

정답 코드 - 방법 2: 비트 연산 활용 C

#include <stdio.h>

int main() {
	int x = 0, y = 0;
	for (int i = 0; i < 3; i++) {
		int a, b;
		scanf("%d %d", 	&a, &b);
		x^=a;
		y^=b;
	}
	printf("%d %d", x, y);
}

비트연산을 활용한 방법이다. ^ 즉 xor연산을 활용한 것인데, xor은 서로 다른 비트일 때 그 결과가 1이 된다.

a	b	a^b
0	0	0
0	1	1
1	0	1
1	1	0

이런 xor의 특성에 따라, 같은 수를 두번 xor하게 되면, 해당 수는 없던 것이 된다. 문제에 적용시켜보면, x1^x2^x1에서 x1^x1을 없앨 수 있고, 결과는 x2가 된다. 따라서 주어지는 각 x와 y좌표를 각각 모두 xor연산을 하게 되면 답이 구해진다.

정답 코드 - 방법 2: 비트 연산 활용 Python 숏코딩

x=y=0;exec('a,b=map(int,input().split());x^=a;y^=b;'*3);print(x,y)